In Progressions:
Arithmetic progression, sequence of numbers such that the difference of any two successive members of the sequence is a constant.
Geometric progression, sequence of numbers such that the quotient of any two successive members of the sequence is a constant.
Arthematic Progression:
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 5, 7, 9, 11, 13, 15 … is an arithmetic progression with common difference of 2.
If the initial term of an arithmetic progression is a_1 and the common difference of successive members is d, then the nth term of the sequence (a_n) is given by:
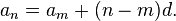
and in general

A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression. The sum of a finite arithmetic progression is called an arithmetic series.
The behavior of the arithmetic progression depends on the common difference d. If the common difference is:
Geometric Progression:
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. The sum of the terms of a geometric progression, or of an initial segment of a geometric progression, is known as a geometric series.
Thus, the general form of a geometric sequence is

and that of a geometric series is

where r ≠ 0 is the common ratio and a is a scale factor, equal to the sequence's start value.
Arithmetic progression, sequence of numbers such that the difference of any two successive members of the sequence is a constant.
Geometric progression, sequence of numbers such that the quotient of any two successive members of the sequence is a constant.
Arthematic Progression:
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 5, 7, 9, 11, 13, 15 … is an arithmetic progression with common difference of 2.
If the initial term of an arithmetic progression is a_1 and the common difference of successive members is d, then the nth term of the sequence (a_n) is given by:
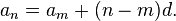
and in general

A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression. The sum of a finite arithmetic progression is called an arithmetic series.
The behavior of the arithmetic progression depends on the common difference d. If the common difference is:
- Positive, the members (terms) will grow towards positive infinity.
- Negative, the members (terms) will grow towards negative infinity.
Geometric Progression:
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. The sum of the terms of a geometric progression, or of an initial segment of a geometric progression, is known as a geometric series.
Thus, the general form of a geometric sequence is

and that of a geometric series is

where r ≠ 0 is the common ratio and a is a scale factor, equal to the sequence's start value.




0 comments:
Post a Comment